Quantum Field Theory
First ideas
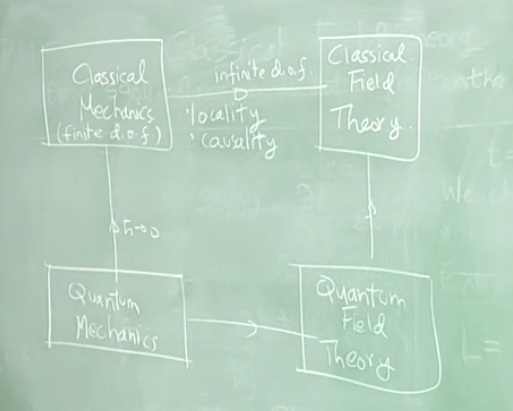
Picture from this video.
Lagrangian point of view
Steps:
1. Lagrangian mechanics for a particle
2. Lagrangian mechanics for several particles: see Lagrangian Mechanics
3. Lagrangian mechanic for a classical field: see Lagrangian field theory
4. Feynman approach to QM for a particle
5. Feynman approach to fields... See also Feynman's path integral formulation.
Old stuff (re read and erase)
We need to generalize Lagrangian Mechanics when we want to deal with a continuum of degree of freedom, in order to obtain locality and causality (I need to understand this yet, but I think that it has to do with action at a distance, and the lack of simultaneity in Special Relativity). This gives rise to Classical Field Theory or, more specifically, Lagrangian field theory. The Quantum Field Theory does the same to Quantum Mechanics: not a discrete set of quantum particles, but a continuum: a quantum field.
Hamiltonian point of view
Quantum Mechanics for particles can be approached from Lagrangian Mechanics (Feynman) or Hamiltonian mechanics (I should review my old notes, starting from here). If we apply the "link" of Hamiltonian mechanics to Quantum mechanics to fields (Hamiltonian field theory) instead of particles, we obtain Quantum Field Theory.
My personal approach
First attempt
Consider, for example, the case of several coupled oscillators, for example 4 of them. We have functions $u_i(t)$ each one describing the position of the $i$th particle. The coupling is reflected by means of an evolution equation defined on a finite dimensional state space (8, in this case, 4 for position and 4 for momentum). When we pass to the wave equation, what we are doing is a transition from a finite amount of degree of freedom to infinite degree of freedom:
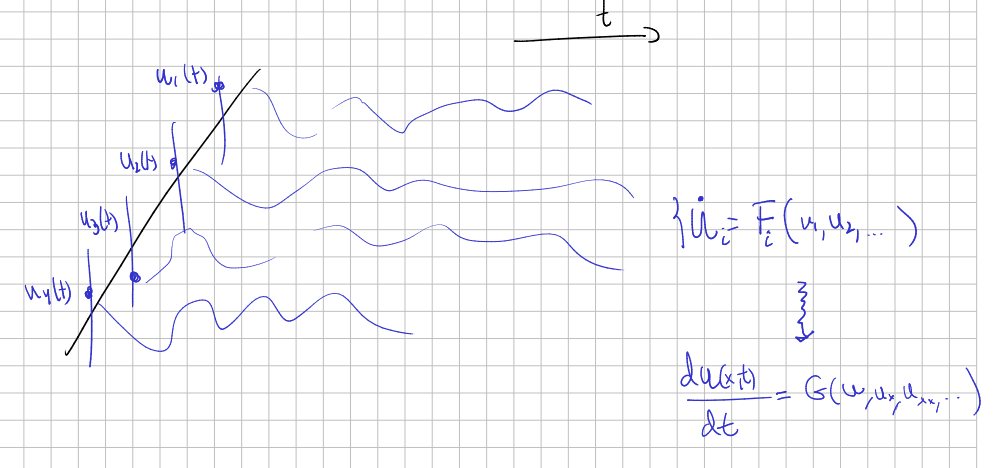
(see this, for more on this).
We are substituting a huge amount of particles by a field.
Now, suppose we study each of the 4 particles from the point of view of Quantum Mechanics. Then we don't have access to, for example, $u_1(t)$ directly, but we have a wavefunction $\Psi_1(u_1,t)$ describing probabilities. BLA BLA BLA continue this, or better, give up and try to transition to QFT from Hamiltonian field theory.
Second attemp
In a Classical Field Theory every point in space (or spacetime) has a field value. In the corresponding Quantum Field Theory, every point in space/spacetime has an operator associated to it. Unlike in Quantum Mechanics, position is not an operator, but a label for the space.
________________________________________
________________________________________
________________________________________
Author of the notes: Antonio J. Pan-Collantes
INDEX: